1. Introduction
Offshore oil platforms are important facilities for offshore oil exploration. Underwater pile grippers play an important role in the construction and installation of platforms. The gripper body is evenly distributed with several hydraulic cylinders in the circumferential direction, and an external oil source provides the hydraulic oil for the hydraulic cylinders. Under the action of hydraulic pressure, the pressure block connected with the plunger holds the pipe pile to provide a horizontal clamping force for the pipe pile, so as to meet the underwater working requirements. When the pile body is supporting the hydraulic cylinder in the working process, the pile body should not only meet the strength requirements, but also ensure that the body is deformed within a certain range [1]. Therefore, the optimum design of the body structure is of great value to ensure that the pile gripper works safely and reliably. In recent years, scholars have conducted finite element analysis on the gripper from the structure of the body, the sealing performance of the hydraulic cylinder, to the gripping manner of the clamping jaws. Sun and Meng [2-3] used ANSYS software to optimize the design of the pinch teeth of the pile gripper, where the tooth profile of the pressure block was optimized, and the maximum stress was reduced by 22.98%. Liang [4] used the ANSYS software to design the gripper. The number of hydraulic cylinders suitable for the structure of the gripper was obtained, and the results of the satisfactory structure of the body were obtained. Jiang, Fang, and Wang [5-7] studied the gripping performance of the underwater gripper, and the relationship between the friction coefficient and gripper angle for the gripper and the pipe pile was obtained. The size of the press block, the optimized structure characteristics of the press block, and the stressed state were improved. Jiang [5,8] analyzed the load on the offshore platform, the working principle of the hydraulic system of the gripper, and designed a hydraulic circuit that met the needs of holding. Finally, a control system that satisfies the requirements using a PID control algorithm was obtained. Sun [8-9] used the finite element software to design and optimize the hydraulic cylinder snap ring. The contact finite element design method was used to simulate the force condition of the snap ring and optimize the design of the structure of snap ring. The snap ring equivalent stress is reduced by 7MPa. The design and optimization of the gripper are mainly realized by using finite element software. The existing research results involve optimization design of the body of the pile gripper, and the main analysis focuses only on the diameter of the piles. In this paper, ANSYS software was used for structural design and size optimization of the body of the gripper. Under the condition of satisfying the structural rigidity requirements, the requirements for minimum equivalent stress and minimum volume of the pile body were achieved.
2. Working Principle of Underwater Pile Gripper
Figure 1
Figure 1.
Installation instruction of the pile gripper
Figure 2
Figure 2.
Structure diagram of the pile gripper
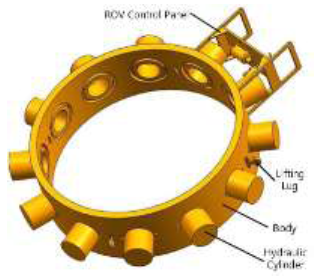
As shown in Figure 1, the pile gripper is sleeved in the pipe pile and the upper end of it is welded to the lower part of the skirt pile sleeve. During the installation of the jacket platform, the leveling machine is used to level the pipe pile, and then the pile gripper starts to work and clamps the pipe pile to provide guarantee for the smooth operation of the subsequent grouting operation. As shown in Figure 2, the underwater skirt pile gripper consists of a body, some hydraulic cylinders, a lifting lug, and a control panel of the Remote Operated Vehicle (simplified to ROV). The body is circumferentially opened in several holes to install and fix a plurality of hydraulic cylinders. In order to facilitate the installation of the pile gripper, the body is uniformly welded with four lugs in the circumferential direction, which facilitates the lifting of the pile gripper when the project is applied. The ROV control panel is welded to the specified location on the body.
3. Force Analysis of the Body
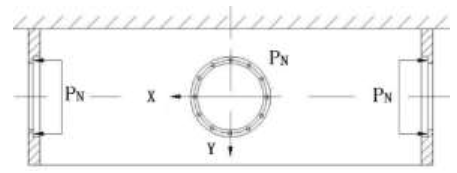
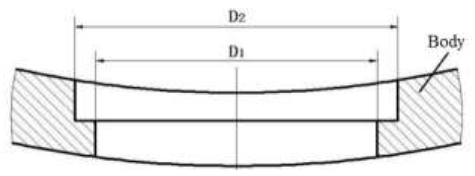
The material of the body is ZG06Cr16Ni5Mc, the elastic modulus E is 200GPa, the Poisson’s ratio is 0.3, the yield limit is 600MPa,the safety factor is 1.5, and the allowable stress is 400MPa. In the working process, the hydraulic cylinders are uniformly distributed on the body clamping the pipe pile. The reaction force of the pipe pile on the hydraulic cylinder acts on the step surface of the body through the flange surface of the hydraulic cylinder. A force diagram of the body of a pile gripper is shown in Figure 3. A diagram of the trapezoidal hole of the body is shown in Figure 4.
Figure 3
Figure 3.
Force diagram of the body
Figure 4
Figure 4.
Trapezoidal hole schematic of the body
The underwater pile gripper provides 1500 tons of clamping force for the pipe pile in the working process. Here, n hydraulic cylinders are evenly distributed around the body. The working pressure of each hydraulic cylinder is P. The press block of pile gripper is connected to the front end of the hydraulic cylinder plunger. When the hydraulic cylinder is working, the press block is pushed out to clamp the pipe pile. According to the working principle of the hydraulic system, the relationship between the number of hydraulic cylinders, working pressure, and clamping force that pile gripper is provided:
WhereF is the clamping force and equals 1500t, and S is the working area of a hydraulic cylinder.
Substituting the data into Equation (1), the relationship between the number of cylinders and the working pressure of the hydraulic cylinder can be obtained with $P=\frac{15}{Sn}$(MPa).
According to Newton’s third law, Equation (2) can be obtained.
Where ${{P}_{N}}$ is the force of the trapezoidal hole of body and ${S}'$ is the area of the trapezoidal hole.
In order to meet the need of grouting, the size of the trapezoidal hole can be preliminary designed: ${{D}_{1}}=\phi 305\text{mm}$ and ${{D}_{2}}=\phi 350\text{mm}\text{.}$ The depth h of the two small holes is the same, which is half the thickness of the body. According to the above parameters, it can calculated by ${S}'=0.023{{\text{m}}^{\text{2}}}$. It can be obtained by
In order to ensure that the forces around the pipe pile are uniform, n should be an even number. The cylinder number nwas chosen as 6, 8, 10, 12, and 14. The working pressure corresponding to different cylinder numbers is shown in Table 1.
Table 1 Cylinder number and corresponding load
| n | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|
| PN/MPa | 108.7 | 81.52 | 65.22 | 54.35 | 46.58 | 40.76 |
4. Number Analysis of the Holes of the Body
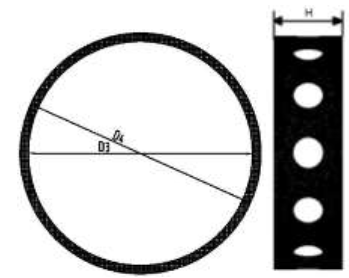
The pipe diameter of the 84-inch pipe pile is $\phi 2134\text{mm,}$ and the body of the pile gripper cannot contact the pipe pile. According to the grouting requirements, the dimensions of the main body of the pile gripper were preliminarily designed as ${{D}_{3}}=\phi 2190\text{mm,}$${{D}_{4}}=\phi 2330\text{mm,}$ and H=700mm. The finite element model of the body is shown in Figure 5.
Figure 5
Figure 5.
Finite element model diagram of the body
Figure 6
Figure 6.
Corresponding stress and strain diagrams of the body for different opening numbersn from 6 to 16
When there are few openings in the pile gripper, the trapezoidal surface of the hole of the body is subject to greater stress. With an increasing number of opening holes, the forceis reduced. It can be seen from Figure 6 that when the number of cylinders n increases from 6 and so on, the stress and strain gradually decrease. When n=12, the effective stress of the body is 286.65MPa, and the equivalent strain is 0.68mm. When the numbers of holes continue to increase, the external force of the trapezoidal surface is reduced, but the distance between each hole decreases and the structural strength decreases. It can be seen from Figure 6 that when n continues to increase, the equivalent stress and strain increase again. Therefore, when n=12, the force of the body structure is reasonable.
5. Structural Optimization of the Body
Even though the development of the pile gripper has been made, the requirements for specific engineering applications are often not fully satisfied. This requires structural optimization after the preliminary design of the pile gripper. The body is evenly distributed with 12 trapezoidal holes in the circumferential direction. A schematic diagram of a trapezoidal hole is shown in Figure 4. The trapezoidal hole of the body is subjected to the external force and is prone to stress concentration. In theory, the greater the difference between ${{D}_{1}}$ and ${{D}_{2}}$, the larger the annular area of the hole of the body and the smaller the ${{P}_{N}}$, which is beneficial to the force of the trapezoidal hole. However, the increase in ${{D}_{2}}$ will reduce the structural strength of the body. Therefore, it is necessary to optimize the size of the trapezoidal holes. For the body, the increase in the inner diameter ${{D}_{3}}$, outer diameter ${{D}_{4}}$, and height H is advantageous for structural strength, but the increase in the size of the structure will reduce the rigidity of the structure.It is not conducive to achieving the goal of a lightweight structure. In order to obtain a more reasonable structure of the pile body, an optimized design is required for the inner diameter, outer diameter, and height of the body [4,10].
5.1. Mathematical Optimization Model of the Body
The circumferential deformation of the body is f1. In order to ensure the safety of the hydraulic cylinder, the equivalent strain of the body needs to meet the stiffness requirement, i.e., ${{f}_{1}}\le 0.01{{D}_{3}}$. In the previous design, the outer diameter of the hydraulic cylinder is $\phi 260\text{mm}$ and the outer diameter of the hydraulic cylinder flange is $\phi 320\text{mm}$. To ensure that the hydraulic cylinder can be installed in the small hole of the body, the conditions $260\text{mm}<{{D}_{1}}<{{D}_{2}}$, ${{D}_{2}}>320\text{mm}$ must be satisfied. The size of the diameter of the 84-inch pipe pile is $\phi 2134\text{mm,}$ and then ${{D}_{3}}$ satisfies the condition ${{D}_{3}}>2134\text{mm}\text{.}$ The minimum value of the maximum equivalent stress ${{\sigma }_{ea}}$and the minimum value of the bulk volume Vwere taken as the objective function. The diameter of the trapezoidal hole ${{D}_{1}}$, major diameter ${{D}_{2}}$, inner diameter of the body ${{D}_{3}}$, outer diameter ${{D}_{4}}$, and height Hare the optimal design variables.
The mathematical optimization model of the body of the pile gripper is:
Where ${{\sigma }_{ea}}$and V are target variables,X is the design variable, and ${{f}_{1}}$ is the state variable.
5.2. Sensitivity Analysis
The sensitivity of the optimization model refers to the degree of influence of the design variables on the output of the model [11]. In this paper, before the optimization calculation, it is necessary to verify that the design variables involved in the optimization model have a significant impact on the ontology equivalent stress and the volume of the ontology, which was used to ensure the selected design variables are reasonable.
The relationship among the target variable V and each design variable is
From Equation (5), it can be seen that the volume of the body is related to the design variables mentioned in Equation (4). The inner diameter, outer diameter, and height of the body are larger, and the influence on the body volume is larger. The size of trapezoidal holes is small and has a little effect on the volume of the body. The above five design variables are valid for the target variable V.
For the target variable ${{\sigma }_{ea}}$, the influence of each parameter quantity is not a simple linear relationship, and it is difficult to obtain a specific functional equation. The optimal gradient method in ANSYS software is the proper method to obtain the maximum equivalent stress sensitivity of the design variables to the body. The sensitivity curves of the parameters to the maximum equivalent stress of the body structure are shown in Figures 7,8,9,10,and 11.
Figure 7
Figure 7.
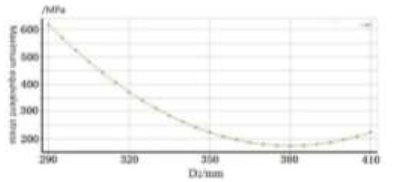
Relationship curve of D1 and equivalent stress
Figure 8
Figure 8.
Relationship curve of D2 and equivalent stress
Figure 9
Figure 9.
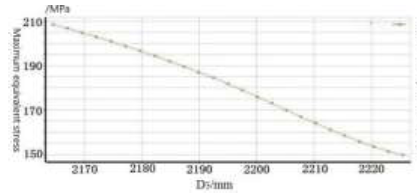
Relationship curve of D3 and equivalent stress
Figure 10
Figure 10.
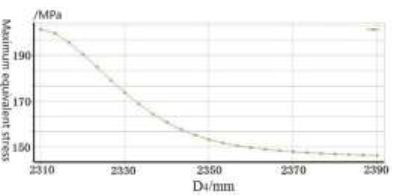
Relationship curve of D4 and equivalent stress
Figure 11
Figure 11.
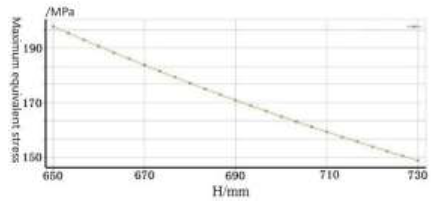
Relationship curve of H and equivalent stress
From Figures 7 to 11, it can be seen that as the diameter of the small diameter ${{D}_{1}}$ increases, the effective stress of the body increases. Because the increase in ${{D}_{1}}$ will reduce the area of the annular surface of the hole, this makes the annular surface stress of the hole ${{P}_{N}}$ increase. When the diameter ${{D}_{2}}$ increases, the area of the annular surface of the small hole increases, the force on the annular surface decreases, and the maximum effective stress of the body decreases.
However, with an increase in the diameter ${{D}_{2}}$ of the hole continuously, the strength of the body structure will decrease. The maximum equivalent stress starts to increase, which is consistent with the previous force analysis results. The change in the small hole size has a significant effect on the maximum equivalent stress of the body. Therefore, ${{D}_{1}}$ and ${{D}_{2}}$ could be selected as the design variables for reducing the maximum equivalent stress.
It can be seen from the above figures that the increase of the inner diameter ${{D}_{3}}$, outer diameter ${{D}_{4}}$ and height H of the body causes the maximum equivalent stress of the structure to decrease. However, the influence of these three variables on the maximum equivalent stress is relatively small. Since the dimensions of the inner diameter ${{D}_{3}}$, outer diameter ${{D}_{4}}$, and height H of the body are large, the influence on the volume of the body is large. Therefore, the inner diameter ${{D}_{3}}$, outer diameter ${{D}_{4}}$, and height H of the body can be selected as the design variables for the lightening of the structure.
5.3. Analysis of Optimization Results
According to the optimization model of Equation (4), the body structure of the pile gripper is optimized. After several iterations, six groups of non-inferior solutions are obtained. The data before and after the optimization are shown in Table 2.
Table 2 Optimization design results of the body
| Program | Original program | Optimization | ||||||
|---|---|---|---|---|---|---|---|---|
| ${{A}_{0}}$ | ${{A}_{1}}$ | ${{A}_{2}}$ | ${{A}_{3}}$ | ${{A}_{4}}$ | ${{A}_{5}}$ | ${{A}_{6}}$ | ||
| Design variable | ${{D}_{1}}$/mm | 305 | 335.53 | 330.21 | 324.5 | 324.47 | 274.5 | 275.19 |
| ${{D}_{2}}$/mm | 350 | 380 | 360.35 | 330.99 | 330.94 | 335.25 | 323.51 | |
| ${{D}_{3}}$/mm | 2210 | 2200.41 | 2207.54 | 2180.23 | 2190.10 | 2220.92 | 2209.66 | |
| ${{D}_{4}}$/mm | 2370 | 2360.68 | 2375.32 | 2320.73 | 2330.24 | 2370.34 | 2360.32 | |
| H/mm | 700 | 675.2 | 700.25 | 710.81 | 698.63 | 702.93 | 685.17 | |
| Target of optimization | V/dm3 | 333 | 303 | 335 | 283 | 278 | 326 | 317 |
| ${{\sigma }_{ea}}$/MPa | 286.65 | 281.32 | 251.88 | 496.37 | 320.12 | 338.37 | 244.37 | |
Since the influence of each parameter on the objective function is inconsistent, it is necessary to adopt an appropriate method to select the best design solution. This paper uses the fuzzy matter-element method [12] to select the best solution to obtain the equivalent stress and minimum volume that meet the requirements. In order to satisfy the calculation, the parameters were defined. ${{x}_{1}}$,${{x}_{2}}$,${{x}_{3}}$, and ${{x}_{4}}$ represent the small diameter of the hole ${{D}_{1}}$,large diameter of the hole ${{D}_{2}}$,internal diameter of the body ${{D}_{3}}$, and outer diameter of the body ${{D}_{4}}$ respectively, and ${{x}_{5}}$ represents the height of body H. The concrete steps of the fuzzy matter element method are as follows.
(1) According to the known dezsign results, the judgment matrix R of this method was first obtained.
Where ${{M}_{i}}$(i =0, 1,
(2) After the matrix R was obtained, the parameters were converted to dimensionless blur values. In this paper, range conversion is the most appropriate method.
The benefit indicatoris
Where ${{x}_{ij}}$ is the corresponding value of ${{M}_{i}}$ in scheme ${{A}_{j}}.$
The cost index is
For the optimized parameters, a smaller maximum equivalent stress and volume of the body are better, and they were selected as the cost index; in other parameters, a small diameter ${{D}_{1}}$ and large diameter ${{D}_{2}}$ mainly affect the equivalent stress, and the impact on the volume of the body is small. An increase in ${{D}_{1}}$ will increase the maximum equivalent stress and therefore should be as small as possible, and it should be selected as the cost index. When ${{D}_{2}}$ increases, the maximum equivalent stress decreases first and then increases. As can be seen in Figure 8, when the inner diameter of the body ${{D}_{2}}$ satisfies the relationship ${{D}_{2}}\le 380\text{mm}$, the maximum equivalent stress decreases with an increase in ${{D}_{2}}$. When the relationship ${{D}_{2}}>380\text{mm}$ is satisfied, the maximum equivalent stress increases with an increase in ${{D}_{2}}$. In the design, the size of ${{D}_{2}}$ satisfies the relationship ${{D}_{2}}\le 380\text{mm,}$ and the maximum equivalent stress decreases with an increase in ${{D}_{2}}$, whichis selected as the benefit index.
The internal diameter ${{D}_{3}}$, outer diameter ${{D}_{4}}$, and height H of the body have little influence on the equivalent stress, while they have a greater influence on the volume of the body. It can be seen from Equation (5) that the body volume increasesas ${{D}_{3}}$ and H increase. Therefore, the smaller the two parameters, the better. The two parameters were selected as the cost index. When ${{D}_{4}}$ increased, the volume of the body was reduced. Therefore, the bigger the parameter, the better the result, and it was selected as the efficiency index. The corresponding membership matrix ${R}'$ is as follows.
(3) The membership matrix was obtained, and then the entropy weight method was used to obtain the weight of each design scheme, which was denoted as a vector ${{W}_{j}}$.
The entropy weight method was used to obtain the weight of each parameter. The weight represents the importance of each parameter in the decision. The greater the weight, the more important the representative parameter. Using this method, the pros and cons of each solution can be analyzed more objectively [13-14]. According to the matrix R and ${R}'$ obtained, the entropy value is calculated according to the definition. If the evaluation object n=7 is known, the entropy of the ith evaluation index is as follows.
Where
${{p}_{ij}}=\frac{1+{{r}_{ij}}}{\sum\limits_{j=1}^{n}{(1+{{r}_{ij}})}}$
In the equation, ${{r}_{ij}}$ is the value in matrix${R}'.$
According to the definition, the available matrixcan be calculated:
${{g}_{i}}=[\begin{matrix} 0.8450 & 0.8324 & 0.8452 & 0.8451 \\ \end{matrix}$$\begin{matrix} 0.8451 & 0.8451 & 0.8449{{]}^{T}} \\ \end{matrix}$
The entropy weight can be obtained:
The number of indicators m=7, from which the vector shown below can be obtained:
${{W}_{j}}=[\begin{matrix} 0.1413 & 0.1526 & 0.1411 & 0.1412 \\ \end{matrix}$$\begin{matrix} 0.1412 & 0.1412 & 0.1414] \\ \end{matrix}$
(4) Calculate the performance vector of each solution:
$P={{W}_{j}}{R}'=[\begin{matrix} 0.126 & 0.132 & 0.135 & 0.132 \\ \end{matrix}$$\begin{matrix} 0.139 & 0.129 & 0.146] \\ \end{matrix}$
Based on the above results, it can be known that the sequence of optimization of the pile gripper body optimization programis ${{A}_{6}}$, ${{A}_{4}}$, ${{A}_{2}}$, ${{A}_{1}}$, ${{A}_{3}}$, ${{A}_{5}}$, ${{A}_{0}}$. Compared with the original structure scheme, these six parameters have been optimized, which shows that the optimization parameter selection is reasonable and the optimization method is feasible. Scheme 6 is the optimal scheme of the optimal design. After the optimization parameters were rounded, the optimization parameter values as shown in Table 3 were obtained.
Table 3. Optimizing parameter values
| ${{D}_{1}}$/mm | ${{D}_{2}}$/mm | ${{D}_{3}}$/mm | ${{D}_{4}}$/mm | H/mm. |
|---|---|---|---|---|
| 275 | 324 | 2210 | 2360 | 685 |
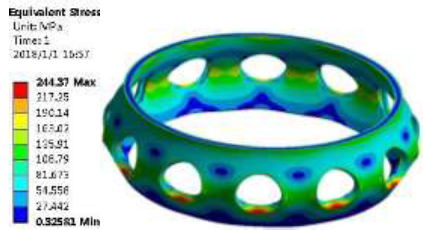
Figure 12
Figure 12.
Stress cloud diagram of optimized body
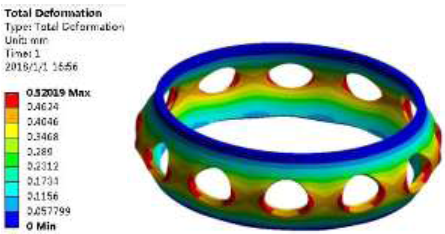
Figure 13
Figure 13.
Strain cloud diagram of optimized body
From Figure 12 and Figure 13, it is known that the maximum equivalent stress of the body is 244.37MPa, which satisfies the strength requirement, and the stress decreases significantly. The maximum equal effect f1 is 0.52mm, which meets the stiffness requirement ${{f}_{1}}\le 0.001{{D}_{3}}=2.21\text{mm,}$ and the maximum equivalent strain hasbeen significantly reduced before optimization.
6. Conclusions
The ANSYS software was selected to analyze and optimize the body of the pile gripper. Through the structural optimization design, it was determined that the 12-holes sleeve body of the 84-inch pile gripper has the best form of stress. Sensitivity analysis was used to determine the choice of smalldiameter of hole ${{D}_{1}}$, large diameter of hole ${{D}_{2}}$, internal diameter of body ${{D}_{3}}$, outer diameter of body ${{D}_{4}}$, and height of body H as the optimal variables. Through optimization analysis, six groups of solutions were obtained, and each parameter was normalized to a dimensionless value using the fuzzy matter-element method. Finally, the optimal design program was completed. After the optimization design of the body, the maximum equivalent stress of the structure was 244.37MPa, which is 14.75% smaller, and the volume of the body was 0.317m3, which is 4.8% smaller. The maximum equivalent stress of the body was reduced by the optimization design in this paper, achieving a lighter and a more reliable guarantee for the safe operation of the pile gripper. The optimization method in this paper provides reference for the design and optimization of the follow-up pile gripper structure.
Acknowledgements
This research is supported by the Central University Fund (HEUCFP201727), Industrialization Application of the Gripper of Jacket Skirt Pile, and Harbin Engineering University Qingdao Ship Science and Technology Co., Ltd.
Reference
Typhoon-Resistant Ultimate Bearing Capacity of Deep-Water Jacket Platforms
,”
Contact Finite Element Analysis of the Pressing Block Tooth in Underwater Skirt Pile Gripper of Offshore Oil Platform
,”Underwater skirt pile gripper was a kind of hydraulic gripper.And it was widely applied in the construction of offshore oil platform.The platform was clamped by pressing block teeth.Augmented Lagrange method combined with finite element analysis was introduced into the pressing block tooth of underwater skirt pile gripper contact design.The body contact design model of pressing block tooth and steel pile was built,and calculated by ANSYS.The contact pressure and extrusion conditions of the pressing block tooth were then obtained,and compared to the theoretical calculation result.The engineering demands were well satisfied.The theoretical basis was provided.And the calculation time was shortened.
Structure Optimization of the Pressing Block Tooth in Underwater Skirt Pile Gripper of Offshore Oil Platform
,”
DOI:10.1109/SIPS.2006.352550
URL
[Cited within: 1]

Underwater skirt pile gripper is a kind of hydraulic gripper.It is widely applied to the construction of offshore oil platform.Tjhe platform is supported by pressing block teeth.Optimal design based on finite element analysis was introduced into the structure of pressing block tooth for underwater skirt pile gripper.The optimal design model was built and calculated by ANSYS.The result of optimal design was gained,and compared to the theoretical calculation result.It was revealed that the application of optimal design process based on finite element analysis was useful in the pressing block tooth of underwater skirt pile gripper design.The structure charoctenstics and force status of the optimal design were improved,and the engineering demands were well satisfied.
Mechanical Analysis of Jacket Pile Gripper and Choice of the Number of Hydraulic Pressure Vats
,”
DOI:10.1016/S1001-6058(07)60030-4
URL
[Cited within: 2]

Pile gripper is the assistant tool for the leveling and grouting of the jacket,and its mechanical analysis is presented in this paper.Compared with the effects on equivalent static coefficient of friction,augmenting the surface roughness of the pincer is a rational method to augment the friction coefficient between pincer and steel pile.And the ANSYS finite element analysis is used to choose the number of hydraulic pressure vats,which are distributed in the pile gripper.
Mechanical Analysis on Underwater Leveling-Gripping System of Jacket and Experimental Research
,”
Analysis and Experimental Study on the Grip Function of an Underwater Skirt Pile Gripper
,”
DOI:10.3969/j.issn.1007-7043.2011.09.023
URL

The underwater skirt pile gripper plays an important part in the installation process of an offshore oil platform jacket.In order to study the clip function,material,and shape of the pressing block in underwater conditions,the skirt pile gripper was investigated.Parameters of the pressing block tooth were designed and optimized,and the contact mechanical model of the pressing block teeth and the steel pile was constructed.The nonlinear relationship between the pressing force and the depth of the pressing block tooth was analyzed by LS-DYNA explicit dynamic analysis.The critical uniform pressing force of the steel pile was ascertained according to the thin shell elastic-plastic stability theory,and the relationship between the pressing force and grip function of the skirt pile gripper was given.The experimental prototype of the skirt pile gripper was developed,experiments were carried out under the actual working conditions,and the effectiveness of the skirt pile gripper was validated by experimental results,providing an effective solution for the problem of large-weight object gripping.
Analysis of Ocean Pile Platform Leveler Clamping Working Mechanism
,”
Check Ring Joint Structure Design in Underwater Skirt Pile Gripper based on Body Contact Nonlinear Finite Element Analysis
,”
DOI:10.1016/S1872-2040(07)60059-0
URL
[Cited within: 2]

Underwater skirt pile gripper(USPG) was a hydraulic gripper widely applied in construction of offshore oil platform.Check ring joint(CRJ) structure was utilized in USPG.Optimization design based on multi-body contract finite element analysis was introduced into structure design of CRJ in USPG.The contact finite element optimization model based on Augmented Lagrange method was established by ANSYS parametric design language(APDL).Optimization results show that this structure optimization method based on nonlinear finite element analysis is effective in joint structure design and the engineering demands are well satisfied.
Structure Optimization Design of Hydraulic Cylinder of Underwater Skirt Pile Gripper of Offshore Oil Platform
,”
DOI:10.1081/MB-100107566
URL
[Cited within: 1]

Optimization design based on finite element analysis were introduced into the hydraulic cylinder design of an underwater skirt pile gripper, and the design was finished. The parametric optimization design model was built in APDL language, and was calculated using ANSYS software. The gained result of optimization design was compared with the result of theoretical calculation. It showed that the optimized structural characteristics and stress states were improved, and the engineering demands were satisfied.
Application of Robotics in Offshore Oil and Gas Industry-A Review PartⅡ
,”
DOI:10.1016/j.robot.2015.09.013
URL
[Cited within: 1]

Demands for oil and gas are increasing with urbanization and industrialization of the world increasing population. Giant oil fields are declining in their production worldwide and this situation is creating need for search of new conventional and non-conventional fossil reserves. With steep depletion of major onshore and shallow-water-offshore oil fields new search of fossil fuel is moving towards deep-water and ultra-deep water offshore fields. Obviously new reserves are located in extreme, hostile and hard-to-reach environmental conditions. Exploration, development and production of oil from such difficult offshore fields have many serious challenges to health, safety and environment (HSE) therefore, require sophisticated technological innovations to support increasing energy demand. Biggest oil spill accidents in explosion of Deepwater Horizon offshore oil platform are burning example of such challenges which human society cannot risk to repeat. Therefore, development of advance drilling system, more accurate and intelligent inspection mechanism, faster responsive system in cases of unfortunate incidence and efficient damage control system is need of the safer future. Successful implementation of robotics, in space and manufacturing industry, is an critical example of how robotic assistance and automation is the only option for safe and cost-effective production of oil in foreseeable future. Teleoperation of unmanned drilling and production platforms, remote operated vehicles (ROVs), autonomous underwater vehicles (AUVs), under-water welding, welding robots for double hulled ships and under-water manipulator are such key robotic technologies which have facilitated smooth transition of offshore rigs from shallow waters to ultra-deep waters in modern time. Considering the sensitivity of product and difficulty of environment, most of these technologies fall under semi-autonomous category, where human operator is in loop for providing cognitive assistance to the overall operation for safe execution. This paper summarizes the key robotic technologies currently used in offshore oil and gas facilities.
Optimization Design of Pressing Machine Frame by ANASYS Workbench Software
,”
Structural Optimization for Rack of Boat-Type Tractor based on Sensitivity Analysis
,”
DOI:10.11975/j.issn.1002-6819.2016.12.008
URL
[Cited within: 1]

In order to promote the mechanization of cultivation in paddy field, Chinese scholars have been devoted to the study of the boat-type tractor. The hull was the main load-carry part of the Chinese traditional boat-type tractor, and modifying the shape and size over and over again based on the experience was the conventional design method of the hull. However, it was hard to ensure the parameters of the static and dynamic property selected from a series of variable ranges were the optimal ones. In order to achieve superior static and dynamic performance of the boat-type tractor, the multi-objective optimization design was conducted on the established separable boat-type tractor rack. The supporting device of the established boat-type tractor was the rack, and the transmission was mounted on it. The transmission was powered by the engine, and then power was output to the gearbox and transfer case through the propeller shaft and finally to the driven wheels. Therefore the rack played an important role in guaranteeing the reliability and stability of the whole machine. First, pre-processing was operated; we extracted the middle surface from the three-dimensional(3D) model and assigned shell units. Full constraint was applied on the rack where the wheels were connected, and after this the finite element analysis of the constraint model was conducted on the rack. Through the modal analysis we found that the first-order modal frequency of the frame was close to the engine working frequency, and therefore we determined the first-order modal frequency as the optimized response. Due to the complexity of the rack structure, we analyzed the sensibility of thickness to the first-order modal frequency, and tank bracket, Beam 1, Beam 2, gearbox bracket, Beam 3, Beam 5 and main beam were defined as the design variables. Besides, we took the minimum volume as the optimization goal. Then, the multi-objective optimization design model was established and 6 groups of non-inferior solutions were obtained. In order to select the optimal design scheme from 6 groups of non-inferior solutions, we composed complex fuzzy matter-element matrix of characteristics and their corresponding values in the optimized system. After normalizing the matrix, the membership matrix was acquired. This matrix could help us determine the entropy weight of the evaluation indices, and thus we could get the advantages and disadvantages of each non-inferior solution. After obtaining the optimal solution, we redesigned the rack and carried out the modal analysis, and the statics check was also conducted on it. Comparing the results before and after optimization, we found that the first-order modal frequency increased from 25.78 to 34.84 Hz whose growth rate was more than 35%, the maximum static stress decreased from 51.18 to 37.75 MPa, and moreover the working frequency of the engine was away from the natural frequency of the boat-type tractor rack. The most important thing was that at the time we obtained the excellent performance of the rack the volume of the rack only increased by 2.4%. The result showed that the rack of the boat-type tractor optimized based on the fuzzy matter-element model and coefficient of entropy had good dynamic performance. The research provides theoretical and technical references for the design of the new boat-type tractor.
Suspension Setting for Optimal Ride Comfort of Off-Road Vehicles Travelling on Roads with Different Roughnessand Speeds
,”
DOI:10.1016/j.jterra.2006.05.002
URL
[Cited within: 1]

This paper reports on an investigation to determine the spring and damper settings that will ensure optimal ride comfort of an off-road vehicle, on different road profiles and at different speeds. These settings are required for the design of a four stage semi-active hydro-pneumatic spring damper suspension system (4S). Spring and damper settings in the 4S can be set either to the ride mode or the handling mode and therefore a compromise ride-handling suspension is avoided. The extent to which the ride comfort optimal suspension settings vary for roads of different roughness and varying speeds and the levels of ride comfort that can be achieved, are addressed. The issues of the best objective function to be used when optimising and if a single road profile and speed can be used as representative conditions for ride comfort optimisation of semi-active suspensions, are dealt with. Optimisation is performed with the Dynamic-Q algorithm on a Land Rover Defender 110 modelled in MSC.ADAMS software for speeds ranging from 10 to 50 km/h. It is found that optimising for a combined driver plus rear passenger seat weighted root mean square vertical acceleration rather than using driver or passenger values only, returns the best results. Results indicate that optimisation of suspension settings using one road and speed will improve ride comfort on the same road at different speeds. These settings will also improve ride comfort for other roads at the optimisation speed and other speeds, although not as much as when optimisation has been done for the particular road. For improved ride comfort damping generally has to be lower than the standard (compromised) setting, the rear spring as soft as possible and the front spring ranging from as soft as possible to stiffer depending on road and speed conditions. Ride comfort is most sensitive to a change in rear spring stiffness.
Fuzzy Matter-Element Evaluation of Ore-Rock Capability in Block Caving Method
,”In order to evaluate the cavability of ore-rocks in block caving method,fuzzy mathematics and matter element analysis method were combined together. The cavability of ore-rocks was divided into five grades including none,poor,fair,good and perfect as the types of matters elements. The RQD,the saturated uniaxial compressive strength,the distance of joint,the hydraulic radius of first cut and the hydraulic feature values were taken as the indices of evaluation. Based on the principle of membership degree in fuzzy evaluation analysis,the membership degree of ore-rock index relative to different evaluation categories were calculated. A model of cavability of ore-rocks in terms of complex fuzzy matter element analysis was established;and a method of cavabiltiy description was presented. The cavability of ore-rocks in a copper-molybdenum mine at the Jiuding mountain was evaluated with the proposed method. The results indicate that:the cavability of altered hornfels is fair;the cavability of altered granite porphyry is good;and the cavability of dense granite porphyry is poor. The results of the evaluation agree well with results of ore lumpiness monitoring and avoided the problem of incompatibility of the evaluation with a single factor index.